Tame tangles, singularities, and Morse theory
Abstract. Classical singularity theory and higher category theory have tantalizing connections: via the generalized tangle hypothesis we can understand singularities as expressing categorical laws satisfied by dualizable objects. However, classical singularity theory, based in differential-topological foundations, encounters technical problem in higher dimensions, which stalls this connection. Using our technology of manifold diagrams we outline steps towards remedying the problem, paving the way towards “higher” Morse theory.
This note is part of a series.
UPDATE. A new paper appeared, which formally introduces tame tangles.
Tangles
A \(k\)-tangle in codimension \(i\) is a \(k\)-manifold with boundary embedded in the closed \((i+k)\)-cube \(\textbf{I}^{i+k}\) (more precisely, the manifold has “corners” which land in appropriate parts of the boundary of the cube). Figure 1 shows a \(1\)-tangle in the \(3\)-cube, and thus in codimension \(2\).
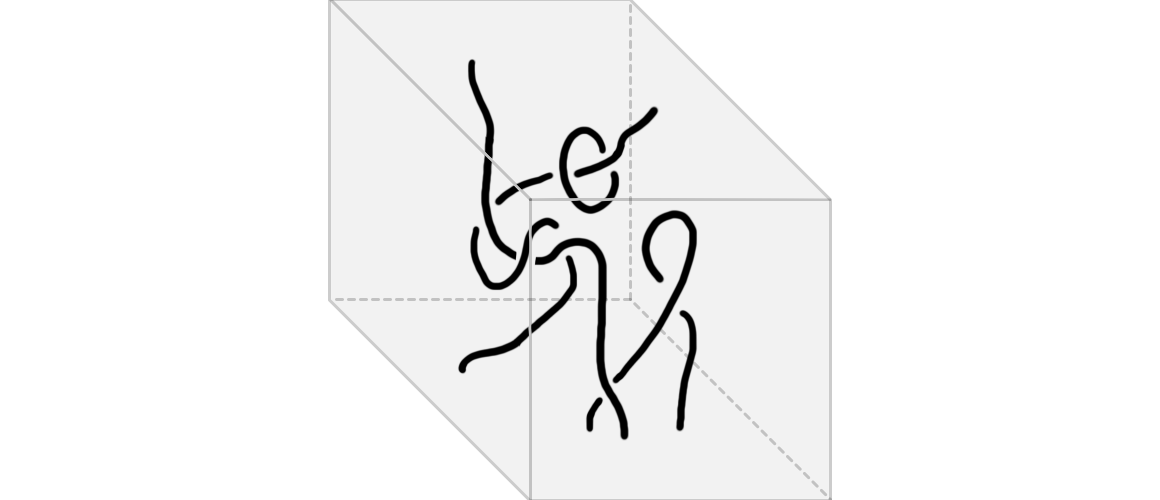
Tame tangles
We will be interested in tangles that are “tame”.
Intuitively, the condition of tameness will exclude tangles that have infinitely many critical points. Importantly, this applies at “all categorical levels”. First, the tangle itself (thought of as endowed with a function to \(\mathbb{R}\) by projecting \(\textbf{I}^n = \textbf{I} \times \textbf{I}^{n-1} \to \textbf{I}\) to the first component of the cube) must have only finitely many critical points. More generally, all stratifications obtained by projecting the tangle along \(\textbf{I}^n = \textbf{I}^k \times \textbf{I}^{n-k} \to \textbf{I}^k\) to lower dimensional cubes must also have only finitely many critical points. For example, the tangle in Figure 2 consisting of two strands colored in blue and red is not tame: its projection to the 2-cube \(\textbf{I}^2\) has infinitely many intersection points (it thus has infinitely many critical points, i.e. points at which the topology of the stratified level sets \(\{t\} \times \textbf{I}^1 \subset \textbf{I}^2\) locally changes for \(t \in \mathbf{I}\)).
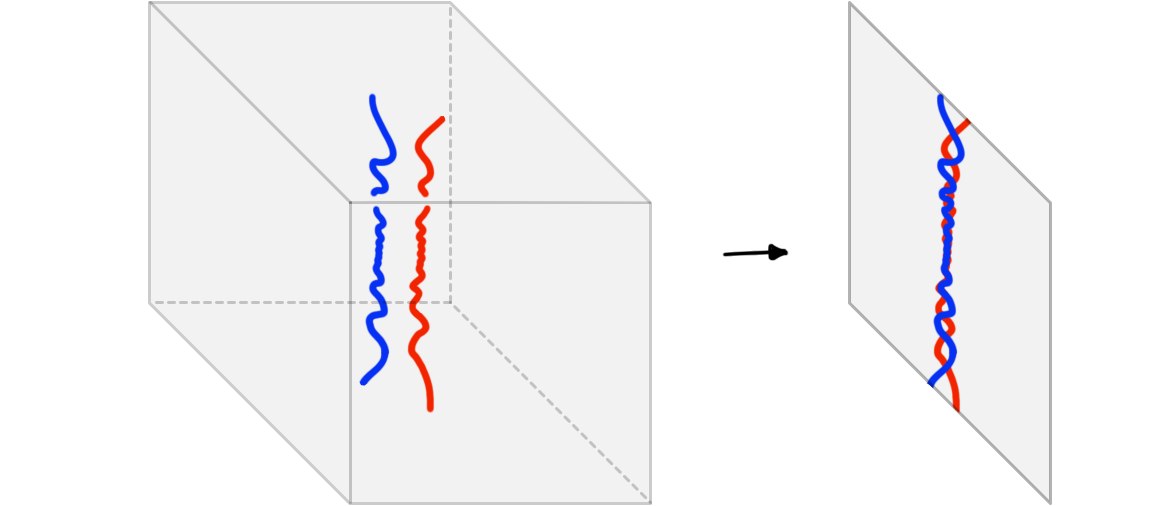
Formally, the condition of tameness is defined as follows. Recall, a manifold \(n\)-diagram is a framed conical stratification that is globular and tame. Here, tameness precisely means that manifold diagrams are refinable by a “mesh” of finitely many framed stratified disks.
Definition. A tame tangle is a tangle that can be refined by (the closure of) a manifold diagram.
Importantly, we may perturb our example of a non-tame tangle slightly to resolve the infinitely many intersections. We illustrate this in Figure 3. The resulting tangle is tame.
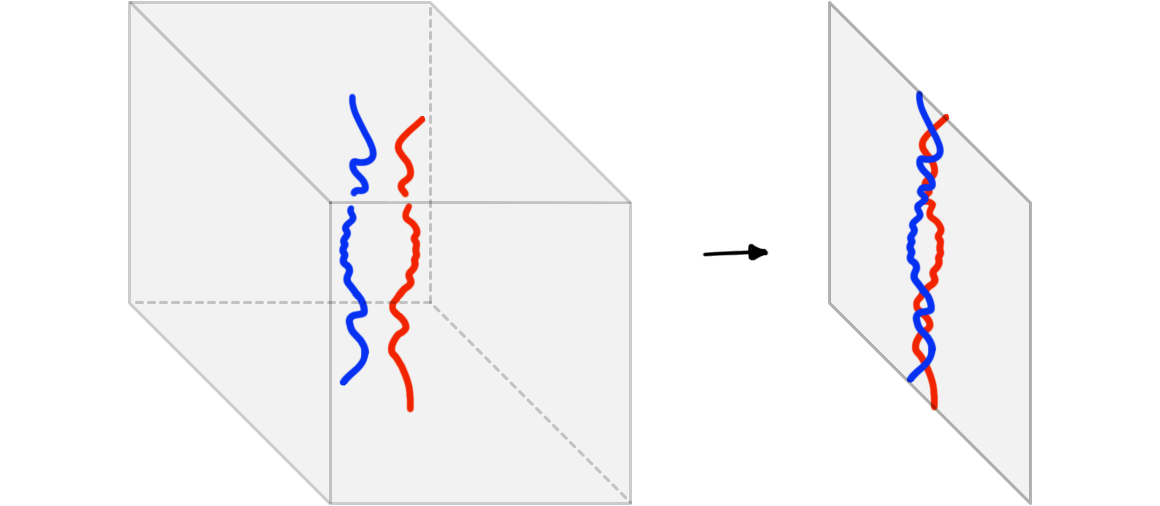
This motivates the following claim.
Conjecture. Every smooth tangle has a (arbitrarily) small perturbation to a tame tangle.
The tangle hypothesis
Tangles form a (higher) category: they compose by appropriately stacking together their ambient cubes. The tangle hypothesis (see also [2] and [3]) translates the category of tangles to a category defined in purely categorical terms. Moreover, it is often regarded as desirable that “purely categorical” entails working in “purely combinatorially” terms.
For tame tangles, this translation into combinatorics becomes trivial owing to the combinatorializability of manifold diagrams. Indeed, each tame tangle has a unique coarsest refining manifold diagram; and each manifold diagram can be dualized to a combinatorial pasting diagram as shown in [1]. This translates tame tangles into pasting diagrams, and thus into categorical combinatorial data.
The relevance of this translation stems from the tangle hypothesis being a guiding principle in understanding “categorical dualizability laws”. (Furthermore, structured variations of the geometric notion of tangles yield various variations of the notion of dualizability in category theory.) Of particular interest in this regard are tangle singularities, which are tangles that translate into a pasting diagram with a single cell. We will next explore a particularly important case of tangle singularities, given by so-called elementary singularities.
Stabililty
Classical singularity theory is concerned with questions of “genericity” of functions. For instance, a classical Morse function is a generic 1-function on a manifold. A classical Morse-Cerf function, is a generic path in the space of 1-functions. Genericity can be understood as a “stability” condition: a small perturbation of a Morse function is again a Morse function (in fact, the space of Morse functions is open in the space of 1-functions); and similarly, a small perturbation of a Morse-Cerf function is again a Morse-Cerf function.
Perturbations of tame tangles
We can mirror the concept of stability/genericity in the setting of tame tangles. If a tangle can be perturbed to a different tangle, we take this as an indication that the former tangle is less stable than the latter tangle. (The notion of “perturbations” of tangles can be easily defined both topologically and combinatorially, but we won’t go into details here; roughly speaking, a perturbation of an \(n\)-tangle \(t\) is a stratified bundle of \(n\)-tangles over the stratified interval \(\{0\} \subset [0,1]\) whose fiber over \(0\) is the tangle \(t\).)
It remains to distinguish the relations “less stable” and “strictly less stable”. A perturbation witnesses a strict stability comparison if the perturbing tangle is structurally strictly simpler than the tangle that is being perturbed; structural simplicity can be measured in terms of the complexity of cells involved in the corresponding pasting diagrams, and thus in purely combinatorial terms. As an example consider Figure 4: the tangle (in fact, tangle singularity) on the left is the “triple saddle” (also called the Monkey saddle). The triple saddle can be perturbed into two ordinary saddles, as shown on the right. This means the right tangle is more stable than the left tangle; and in fact, it is strictly more stable, since saddles are structurally simpler (as cells) than the triple saddle is.
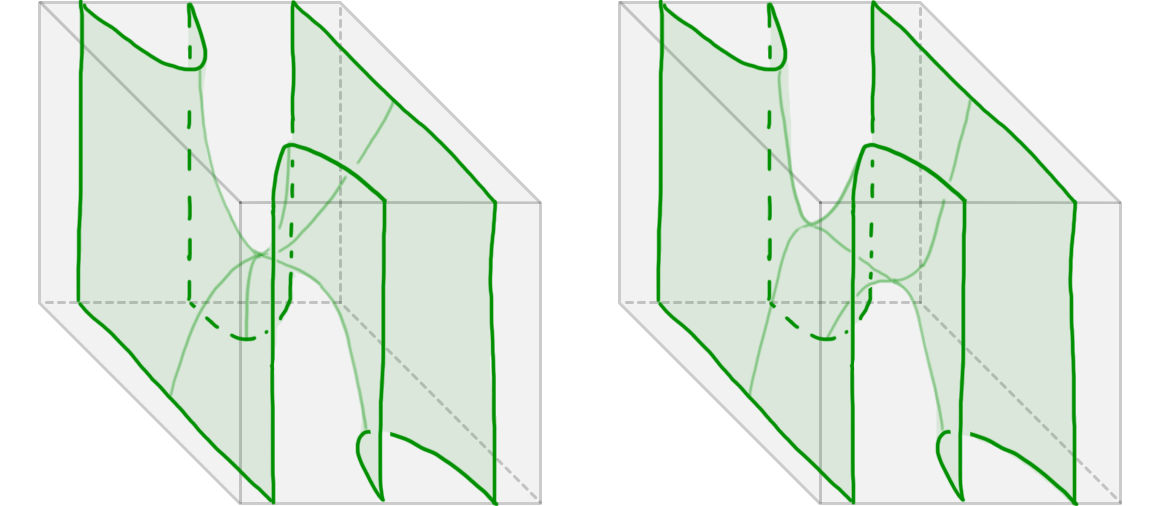
In contrast, any attempt to perturb the saddle into a strictly more stable tangle will fail; indeed, any perturbation of the saddle will itself contain at least one saddle. We say that a tangle which cannot be perturbed to a strictly more stable tangle is perturbation-stable.
It is important to emphasize again that, while the above discussion is motivated in geometric terms, notions of stability of tame tangles can be defined in purely combinatorial terms.
Elementary singularities
A \(k\)-tangle singularity that is perturbation-stable is called an elementary \(k\)-tangle singularity. In Figure 5 we illustrate all elementary \(2\)-tangle singularities in codimension 1.
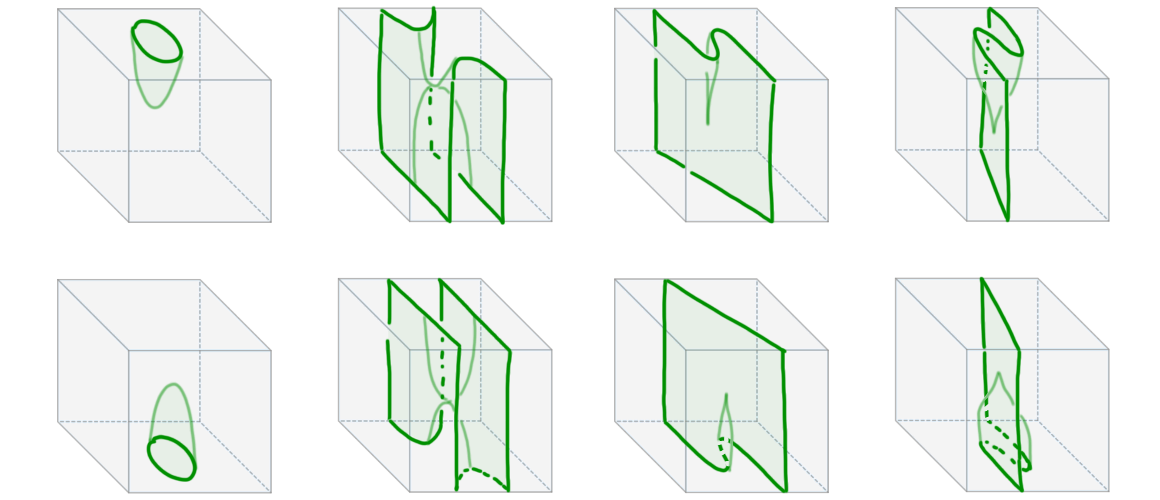
Note that the shown singularities recover the usual Morse singularities (minima, maxima, saddles) and Morse-Cerf singularities (the cusp). This relationship of elementary tangle singularities continues into higher dimensions: many of the classical elementary singularities of Thom and Arnold similarly appear as elementary tangle singularities. (N.B.: in classical singularity theory we often study [\(r\)-parameter families of] 1-functions on \(k\)-dimensional space, whose graphs are codimension 1 hypersurfaces in \(\mathbb{R}^{k+r+1}\) — it is for this reason that the relation of tangle singularities and classical singularities is illustrated here for codimension 1 tangles.)
Importantly however, in higher dimensions, the “combinatorial singularity theory” of tame tangles eventually diverges from the classical “smooth singularity theory” in fundamental ways. The smooth machinery breaks down for higher parameter families, leading to uncountably many equivalence classes of singularities (see Sec. 7.6 in [4])—an issue which traditionally has been addressed in various ways on a case-by-case basis. In contrast, the combinatorial approach to elementary singularities is robust in all dimension.
Not much is known about elementary tangle singularities in general dimension. Extrapolating from lower dimensional cases (and keeping in mind that elementary singularities translate into algebraic laws of dualizable objects in higher category theory) we do conjecture the following.
Conjecture. There are finitely many elementary tangle singularities in each dimension and codimension.
Stratifying the space of tangles
Morse functions (on a given manifold) form the codimension 0 stratum of a stratification of the space of 1-functions. The codimension 1 stratum is given by those 1-functions that Morse-Cerf functions (as paths in the space of 1-functions) pass through, but which are not themselves Morse functions. In principle (and issues of smooth singularity theory aside), one could attempt to continue in this way, constructing a stratification of the space 1-functions whose strata are ordered by their “stability”.
The idea may be realized in the case of (tame) tangles. The space of tangles is the classifying space of the category of tangles and perturbations. Its “stratification by stability” is defined by its non-trivial exit paths: a non-trivial exit path (“non-trivial” meaning the path runs between different strata) is exactly a perturbation from a tangle to a strictly more stable tangle. Note that all elementary tangle singularities live in the codimension 0 stratum of this stratification.
Towards higher Morse theory
The idea of stratifying the space of tangles is closely related to the idea of higher Morse theory. An \(n\)-Morse function is a generic path of (almost) \((n-1)\)-Morse functions. The adjective “almost” indicates that the path may pass through non-Morse \((n-1)\)-functions at a finite set of critical points (but only “generically” so). It turns out, that it is hard to make the idea of higher Morse functions precise using classical smooth machinery.
The combinatorial-topological world of tangles provides a different approach—at least in the “embedded” regime of \(n\)-functions on \(m\)-manifolds for \(n\) sufficiently larger than \(m\). Namely, an embedded \(n\)-Morse function on an \(m\)-manifold \(M\) is an embedding \(M \hookrightarrow \textbf{I}^n\) of \(M\) into the \(n\)-cube \(\textbf{I}^n\) that defines a perturbation-stable \(m\)-tangle in codimension \((n-m)\). More generally, we may then define a (non-embedded) \(k\)-Morse function \(M \rightarrow \textbf{I}^k\) to be a function that can be (non-uniquely) factored through an embedded \(n\)-Morse function \(M \hookrightarrow \textbf{I}^n\) and the projection \(\textbf{I}^n = \textbf{I}^k \times \textbf{I}^{n-k} \to \textbf{I}^k\). Note again, that this definition may be equivalently be given in purely combinatorial terms.
Project. While the theory developed in [1] mainly deals with the embedded case, the following is certainly an interesting question: can we combinatorially define \(k\)-Morse functions without reference to embedded Morse functions?
There are several reasons why one would consider \(n\)-Morse functions in place of traditional \(1\)-Morse functions (see e.g. [5] for a use case of 2-Morse functions). One important reason is the detection of smooth structures. Namely, given an smooth \(m\)-manifold equipped with an embedded \(n\)-Morse function, then the datum of its elementary singularities (and its elementary isotopies, which together define the resulting perturbation-stable tangle) should be able to encode the smooth structure of the manifold—this stands in contrast to the datum of singularities associated to a 1-Morse function, which cannot generally detect smooth structures (instead, these can be “hidden away” in exotic sphere diffeomorphisms of handle attachments).
Crucially, combining this with fact that our approach to higher Morse theory outlined above is combinatorial (in particular, tame tangles are categorical pasting diagrams), this would provide a combinatorialization of smooth phenomena—this realizes the decades-old idea of a combinatorial (or “algebraic”) foundation for smooth structures, dispensing of the need to refer to the continuum \(\mathbb{R}\) (see Sec 5.3 in [1] for further discussion).
References
[1] “Framed combinatorial topology”, Dorn + Douglas
[2] “Higher-dimensional Algebra and Topological Quantum Field Theory”, Baez + Dolan
[3] “On the Classification of Topological Field Theories”, Lurie
[4] “Catastrophe Theory and its Applications”, Poston + Stewart
[5] “The Classification of Two-Dimensional Extended Topological Field Theories”, Schommer-Pries
